01說明
在本例中�,我們仿真了使用BaTiO2的鐵電波導調制器���,BaTiO2是一種折射率因外加電場而發(fā)生變化的材料���。該器件的結構基于文獻[1]�。我們模擬并分析了給定工作頻率下波導調制器的有效折射率與電壓的關系��。

02背景
鐵電波導由硅層和玻璃襯底上的BiTiO3(也稱為BTO)層組成��。BiTiO3晶體的取向為晶體的[011]方向平行于光傳播方向(y方向)����,[001]方向沿著z方向�����。BiTiO3層的頂部的非晶硅可以形成脊波導結構�,可以限制橫向(x方向)的光分布。金電極觸點被放置在離非晶硅脊波導兩側1μm遠的地方�。
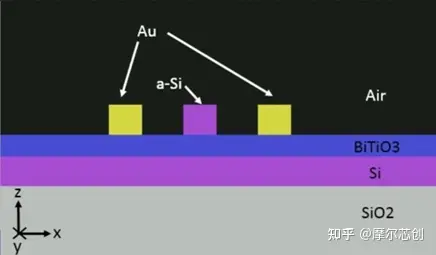
在本案例中,我們首先使用CHARGE求解器模擬不同偏置電壓下���,波導橫截面上的電場分布���。然后�����,我們根據對應的電場分布變化來計算BiTiO3材料折射率的變化���,并模擬分析出不同偏置電壓下波導的有效折射率。
步驟一:用CHARGE模擬電場分布
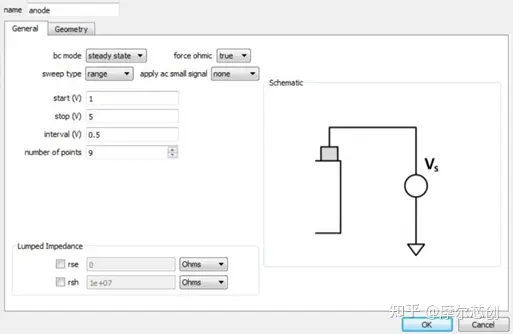
在建立好模型后�����,我們將陰極觸點設置為定值0 V��,陽極觸點設置為掃描模式����,掃描范圍為1-5 V,掃描點間隔為0.5 V���。
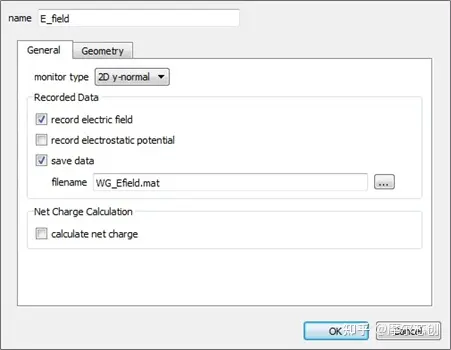
設置完成后����,運行仿真程序將自動進行模式����,掃描結果將由電場監(jiān)視器記錄并將數據保存在WG_Efield.mat文件中���。
步驟二:使用MODE分析有效折射率
為了計算不同電壓下鐵電波導的有效折射率,我們需要使用MODE模塊中的FDE求解器���。FDE求解器可以分析出各類波導橫截面上的導模和導模對應的各類光學參數�����,因此在本步驟中,我們可以使用FDE求解器分析出鐵電波導橫截面有效折射率與偏置電壓的關系圖�����。首先�,我們將上一步中得到的包含不同偏置電壓下電場分布的WG_Efield.mat文件,通過預留的接口導入到FDE求解器中�,如下圖所示。
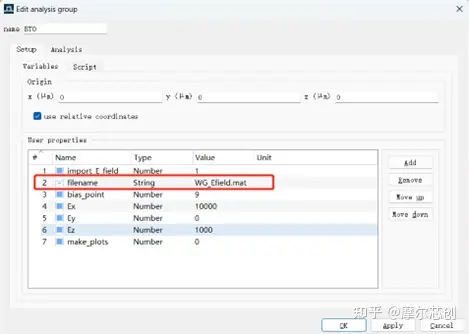
在實現電場數據的傳遞后���,可以通過控制偏壓參數(圖中bias_point)來切換不同電壓下的電場分布�。這樣我們只需要對偏振參數進行掃描���,就能得到不同電壓下鐵電波導的有效折射率���。需要說明的是Lumerical計算不同電場分布對BaTiO2材料折射率的影響是通過編寫腳本程序實現的��,可在上圖setup-script中查看詳細處理過程�。如果使用者需要替換其它鐵電材料或者改變鐵電材料波導傳播方向與電場的角度��,可根據使用情況對腳本程序進行對應修改����。
掃描完成后,可通過腳本程序提取出波導的有效折射率與偏置電壓的關系曲線�����,如下圖所示:
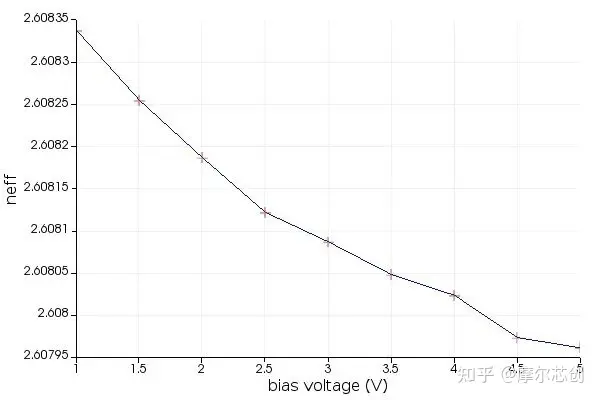
參考說明:
模擬區(qū)域設置
在 CHARGE 中��,半導體區(qū)域必須具有電壓邊界條件�。電壓邊界條件可以直接來自金屬接觸或通過相鄰的半導體層。在上述器件中����,晶體硅層與陽極和陰極接觸絕緣。因此它沒有電壓邊界條件�。為了提供邊界條件��,我們使用接地觸點 (gnd)�。但是我們不希望接地觸點設置的電勢影響陽極和陰極觸點下方的硅板的行為�����。這就是為什么“gnd”觸點需要放置得很遠���,以便陽極/陰極觸點正下方的硅板中的電勢僅由施加在這些觸點上的電壓控制�。與上述相同的原因��,波導中的Si層也需要電壓邊界條件����。我們不是直接從觸點(gnd) 提供邊界條件���,而是通過另一個半導體區(qū)域提供邊界條件���。因此,我們創(chuàng)造了帶隙和介電常數等于 BTO 的大帶隙半導體�,這種半導體版本的 BTO 會將波導中的硅層連接到晶體硅層,從而為其提供電壓邊界條件�。
BiTiO3結構細節(jié)
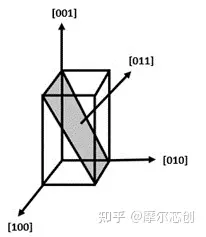
BiTiO3晶體為四方晶系晶體��,在[100]和[010]方向具有尋常折射率no�����,在[001]方向具有非常折射率ne��。在示例文件中�����,我們使用 no=2.379 和 ne=2.339��。在波導中���,BiTiO3 晶體的取向使得晶體的 [011] 方向平行于沿波導的傳播方向,因此需要旋轉晶體的介電常數張量以解決這一問題��。
在未旋轉晶體的坐標系中(x'��、y'�����、z'分別對應[001]���、[010]���、[001]晶向的主坐標系)���,沒有外加電場的BiTiO3材料的介電常數張量為:
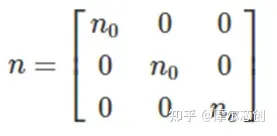
由施加的電場引起的反介電常數張量的擾動由下式給出:
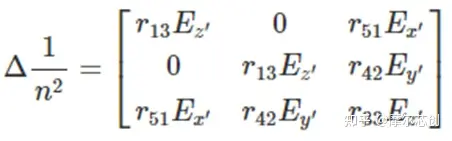
擾動折射率的平方然后由下式給出
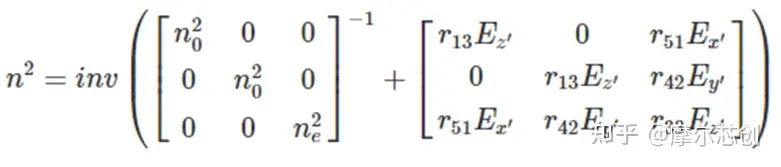
在存在電場的情況下,介電常數張量包含非對角線分量��,我們可以使用對角化介電常數和應用的矩陣變換網格屬性的組合來表示這一點���。這種用非對角分量表示一般介電常數張量的方法在矩陣變換一章中有更詳細的討論��。
矩陣變換文章鏈接:https://optics.ansys.com/hc/en-us/articles/360034915173-Matrix-Transformation-Simulation-object
坐標和旋轉細節(jié)
從參考文獻[1]可知��,BiTiO3的晶格常數為:
a = 3.992 ?
c = 4.036 ?
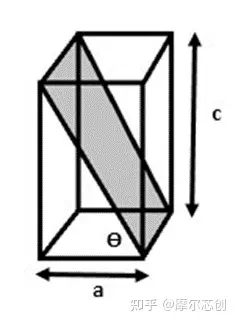
上圖中的 Theta 可以由 ? = arctan(4.036/3.992) 給出
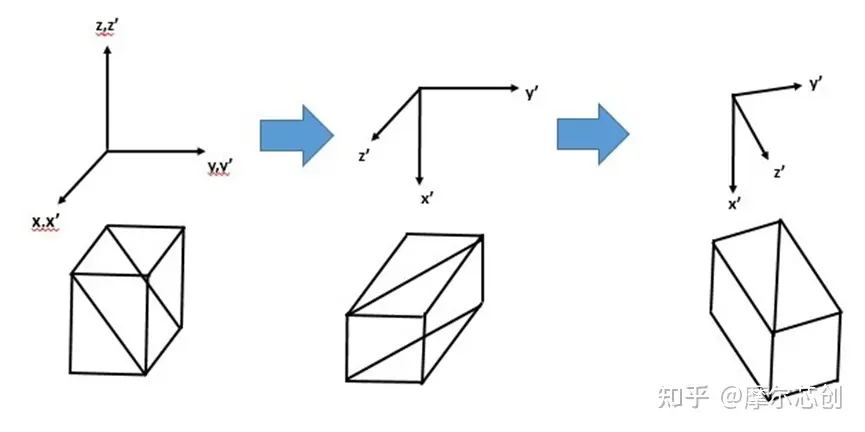
要旋轉晶體的介電常數以使 [011] 方向沿 y���,首先繞 y' 軸逆時針旋轉 pi/2,然后繞新的 x' 軸順時針旋轉 pi/2 - theta�,如下圖所示����。
要計算坐標中的電場,可以使用以下關系:
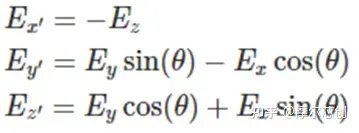
參考文獻:
[1] Chi Xiong, Wolfram H. P. Pernice, Joseph H. Ngai, James W. Reiner, Divine Kumah, Frederick J. Walker, Charles H. Ahn, and Hong X. Tang, “Active Silicon Integrated Nanophotonics: Ferroelectric BaTiO3 Devices”, Nano Letters 2014 14 (3), 1419-1425
翻譯:摩爾芯創(chuàng)-BOb
